Skip to contents

Outputs: Relative effects, forest plots and rankings

Hugo Pedder

2024-07-03

outputs-4.Rmd

Estimating relatived effects between treatments at a specified time-point

Although mb.run() estimates the effects for different treatments on different time-course parameters, these are not necessarily easy to draw conclusions from, particularly for time-course functions with less easily interpretable parameters. get.relative() allows users to calculate mean differences (or log-Ratio of Means if mb.run(link="log")) between treatments at a specified time-point even if a subset, or even none of the treatments have been investigated at that time-point in included RCTs.

These results will then be reported on the scale on which the data were modeled (i.e. depending on the link function specified in mb.run()), rather than that of the specific time-course parameters. Within the matrices of results, mean differences/relative effects are shown as the row-defined treatment versus the column-defined treatment.

# Run a quadratic time-course MBNMA using the alogliptin dataset
network.alog <- mb.network(alog_pcfb)
#> Reference treatment is `placebo`
#> Studies reporting change from baseline automatically identified from the data

mbnma <- mb.run(network.alog, 
                fun=tpoly(degree=2,
                          pool.1="rel", method.1="random",
                          pool.2="rel", method.2="common"
                          )
)
#> module glm loaded
#> Compiling model graph
#>    Resolving undeclared variables
#>    Allocating nodes
#> Graph information:
#>    Observed stochastic nodes: 233
#>    Unobserved stochastic nodes: 71
#>    Total graph size: 4375
#> 
#> Initializing model
# Calculate relative effects between 3 treatments
allres <- get.relative(mbnma, time=20,
                       treats = c("alog_100", "alog_50", "placebo"))
print(allres)
#> ========================================
#> Treatment comparisons at time = 20
#> ========================================
#> 
#>      alog_100       0.9 (0.62, 1.2)    0.83 (-0.5, 2.2) 
#> -0.9 (-1.2, -0.62)      alog_50       -0.064 (-1.4, 1.3)
#> -0.83 (-2.2, 0.5)  0.064 (-1.3, 1.4)       placebo

get.relative() can also be used to perform a 2-stage MBNMA that allows synthesis of results from two different MBNMA models via a single common comparator. In an MBNMA model, all treatments must share the same time-course function. However, a 2-stage approach can enable fitting of different time-course functions to different sets (“subnetworks”) of treatments. For example, some treatments may have rich time-course information, allowing for a more complex time-course function to be used, whereas others may be sparse, requiring a simpler time-course function.

Relative comparisons between treatments in the two datasets at specific follow-up times can then be estimated from MBNMA predicted effects versus a common comparator using the Bucher method and assuming consistency.

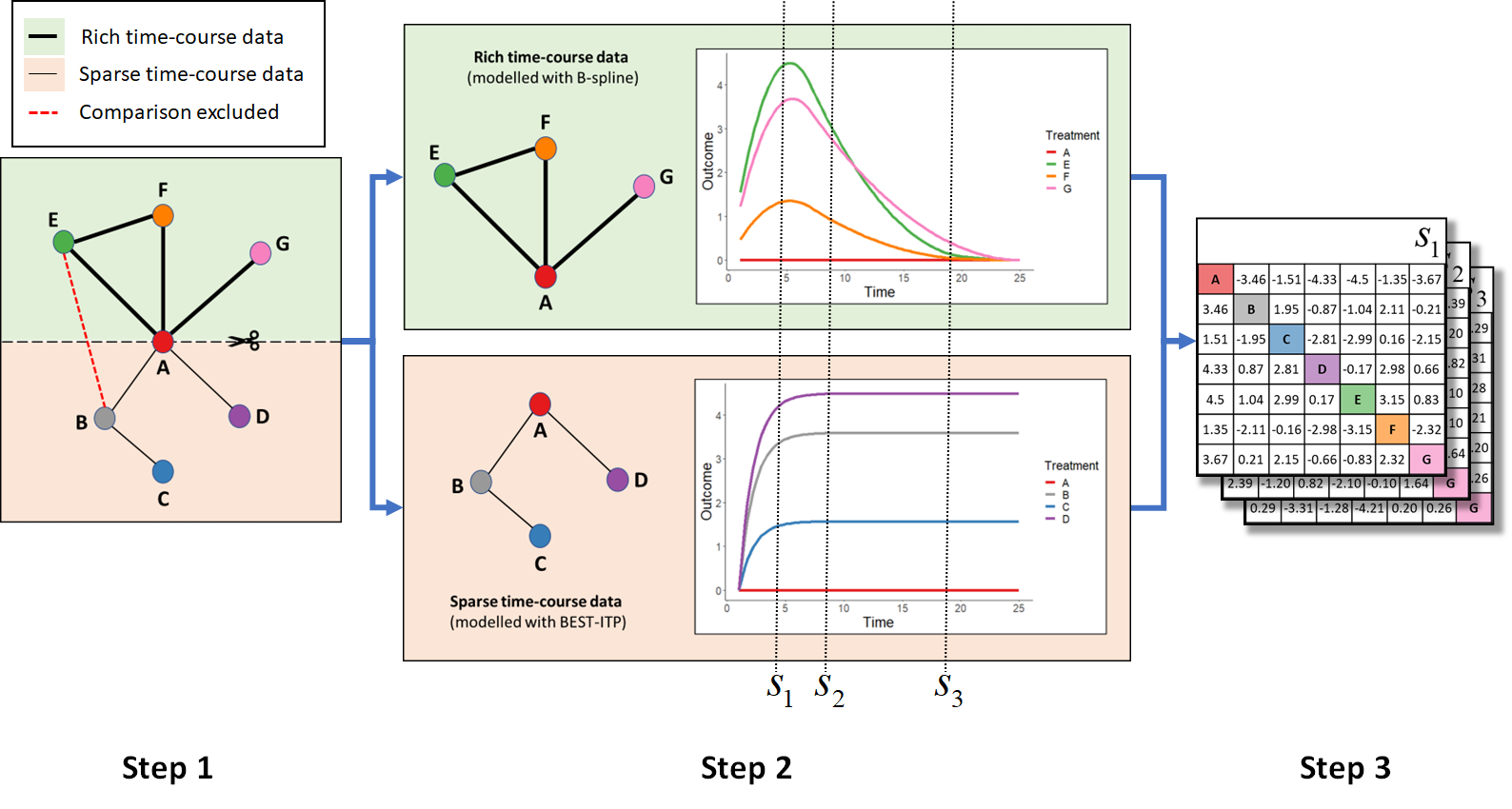
2-stage MBNMA: For clarity, 95%CrIs are not shown in the plots or tables but these are calculated and computed in `get.relative()`. Thick connecting lines in network plots indicate comparisons with rich time-course data that can be modelled with a more complex function (e.g. B-spline), thin connecting lines in network plots indicate comparisons with sparse time-course data that can only be modelled with a less complex function (e.g. BEST-ITP). Comparisons between treatments in different subnetworks that are not the network reference must be excluded (red dashed line in network plot).

2-stage MBNMA: For clarity, 95%CrIs are not shown in the plots or tables but these are calculated and computed in get.relative(). Thick connecting lines in network plots indicate comparisons with rich time-course data that can be modelled with a more complex function (e.g. B-spline), thin connecting lines in network plots indicate comparisons with sparse time-course data that can only be modelled with a less complex function (e.g. BEST-ITP). Comparisons between treatments in different subnetworks that are not the network reference must be excluded (red dashed line in network plot).

  • Step 1: The network at a chosen network reference treatment (A) into subnetworks with rich and sparse time-course data.
  • Step 2: Separate time-course MBNMAs are fitted to each subnetwork using a different time-course function, and relative effects versus the network reference treatment are predicted over time.
  • Step 3: Bucher method is used to calculate predicted relative effects between all treatments at specific time-points of interest (e.g. \({S_{1}}\), \({S_{2}}\) and \({S_{3}}\)). This can be done with get.relative() using the output from both MBNMA models in mbnma and mbnma.add arguments. For more details and an example see the function help file (?get.relative).

Deviance plots

To assess how well a model fits the data, it can be useful to look at a plot of the contributions of each data point to the total deviance or residual deviance. This can be done using devplot(). As individual deviance contributions are not automatically monitored in the model, this might require the model to be run for additional iterations.

Results can be plotted either as a scatter plot (plot.type="scatter") or a series of boxplots (plot.type="box").

# Using the osteoarthritis dataset
network.pain <- mb.network(osteopain, reference = "Pl_0")

# Run a first-order fractional polynomial time-course MBNMA
mbnma <- mb.run(network.pain, 
                fun=tfpoly(degree=1,
                          pool.1="rel", method.1="random",
                          method.power1=0.5))

# Plot a box-plot of deviance contributions (the default)
devplot(mbnma, n.iter=1000)
#> Studies reporting change from baseline automatically identified from the data
#> `dev` not monitored in mbnma$parameters.to.save.
#> additional iterations will be run in order to obtain results for `dev`

From these plots we can see that whilst the model fit is typically better at later time points, it fits very poorly at earlier time points.

A function that appropriately captures the time-course shape should show a reasonably flat shape of deviance contributions (i.e. contributions should be similar across all time points).

If saved to an object, the output of devplot() contains the results for individual deviance contributions, and this can be used to identify any extreme outliers.

Fitted values

Another approach for assessing model fit can be to plot the fitted values, using fitplot(). As with devplot(), this may require running additional model iterations to monitor theta.

# Plot fitted and observed values with treatment labels
fitplot(mbnma, n.iter=1000)

Fitted values are plotted as connecting lines and observed values in the original dataset are plotted as points. These plots can be used to identify if the model fits the data well for different treatments and at different parts of the time-course.

Forest plots

Forest plots can be easily generated from MBNMA models using the plot() method on an "mbnma" object. By default this will plot a separate panel for each time-course parameter in the model. Forest plots can only be generated for parameters which vary by treatment/class.

# Run a quadratic time-course MBNMA using the alogliptin dataset
mbnma <- mb.run(network.alog, 
                fun=tpoly(degree=2,
                          pool.1="rel", method.1="random",
                          pool.2="rel", method.2="common"
                          )
)

plot(mbnma)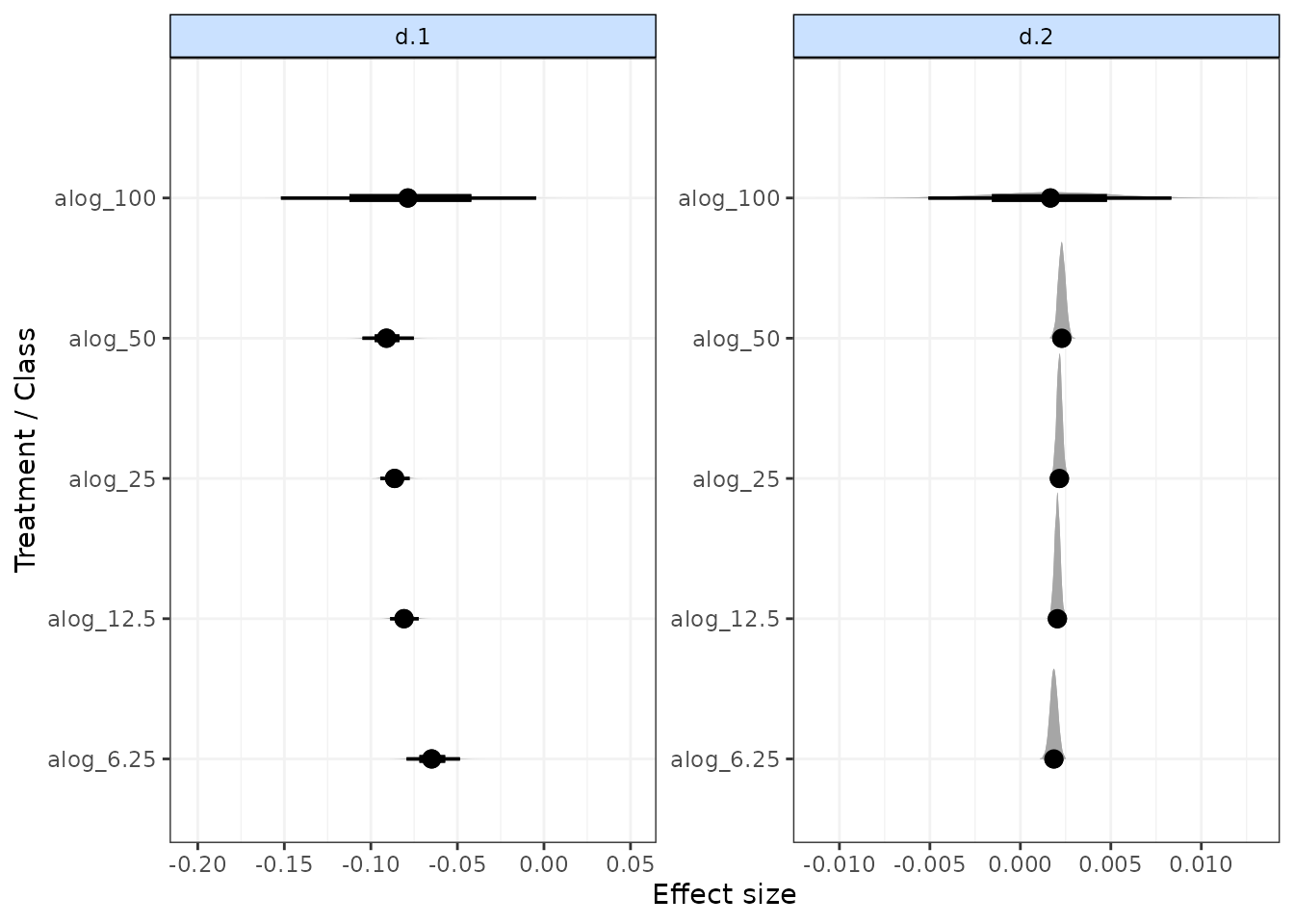

rank(): Ranking

Rankings can be calculated for different time-course parameters from MBNMA models by using rank() on an "mbnma" object. Any parameter monitored in an MBNMA model that varies by treatment/class can be ranked by passing its name to the params argument. lower_better indicates whether negative scores should be ranked as “better” (TRUE) or “worse” (FALSE)

In addition, it is possible to rank the Area Under the Curve (AUC) for a particular treatment by specifying param="auc" (this is the default). This will calculate the area under the predicted response over time, and will therefore be a function of all the time-course parameters in the model simultaneously. However, it will be dependent on the range of times chosen to integrate over (int.range), and a different choice of time-frame may lead to different treatment rankings. "auc" can also not currently be calculated from MBNMA models with more complex time-course functions (piecewise, fractional polynomials), nor with MBNMA models that use class effects.

# Using the osteoarthritis dataset
network.pain <- mb.network(osteopain, reference = "Pl_0")
#> Studies reporting change from baseline automatically identified from the data

# Identify quantile for knot at 1 week
timequant <- 1/max(network.pain$data.ab$time)

# Run a piecewise linear time-course MBNMA with a knot at 1 week
mbnma <- mb.run(network.pain,
                fun=tspline(type="ls", knots = timequant,
                            pool.1 = "rel", method.1="common",
                            pool.2 = "rel", method.2="common"))


# Rank results based on AUC (calculated 0-10 weeks), more negative slopes considered to be "better"
ranks <- rank(mbnma, param=c("auc"), 
                    int.range=c(0,10),  lower_better = TRUE, n.iter=1000)
print(ranks)
#> 
#> ========================================
#> Treatment rankings
#> ======================================== 
#> 
#> auc ranking
#> 
#> |Treatment |  Mean| Median| 2.5%| 97.5%|
#> |:---------|-----:|------:|----:|-----:|
#> |Pl_0      | 26.16|     26|   24| 28.00|
#> |Ce_100    | 21.42|     22|   16| 26.00|
#> |Ce_200    | 13.92|     14|   10| 18.00|
#> |Ce_400    | 13.29|     13|    6| 21.00|
#> |Du_90     | 14.93|     15|    1| 29.00|
#> |Et_10     | 27.12|     28|   19| 29.00|
#> |Et_30     |  6.70|      6|    3| 12.00|
#> |Et_5      | 12.99|     11|    2| 27.00|
#> |Et_60     |  4.26|      4|    2|  8.00|
#> |Et_90     |  7.70|      5|    1| 25.00|
#> |Lu_100    | 13.70|     14|    8| 19.00|
#> |Lu_200    | 15.39|     16|   10| 20.00|
#> |Lu_400    |  9.71|     10|    5| 16.00|
#> |Lu_NA     | 13.89|     10|    1| 29.00|
#> |Na_1000   |  8.34|      8|    5| 13.00|
#> |Na_1500   |  9.17|      9|    4| 16.00|
#> |Na_250    | 27.73|     28|   24| 29.00|
#> |Na_750    | 19.10|     19|   11| 24.00|
#> |Ox_44     |  5.09|      4|    1| 19.00|
#> |Ro_12     | 20.78|     23|    5| 28.00|
#> |Ro_125    |  2.63|      2|    1| 16.02|
#> |Ro_25     | 16.98|     18|    5| 25.02|
#> |Tr_100    | 23.36|     24|   19| 26.00|
#> |Tr_200    | 22.35|     23|   18| 26.00|
#> |Tr_300    | 15.60|     16|    8| 21.00|
#> |Tr_400    | 11.40|     11|    4| 20.00|
#> |Va_10     | 21.26|     22|   13| 26.00|
#> |Va_20     | 13.56|     14|    5| 22.00|
#> |Va_5      | 16.48|     17|    7| 24.00|

The output is an object of class("mb.rank"), containing a list for the ranked parameter which consists of a summary table of rankings and raw information on treatment ranking and probabilities. The summary median ranks with 95% credible intervals can be simply displayed using print().

Histograms for ranking results can also be plotted using the plot() method, which takes the raw MCMC ranking results given in rank.matrix and plots the number of MCMC iterations the parameter value for each treatment was ranked a particular position.

# Ranking histograms for AUC
plot(ranks)

Cumulative rankograms indicating the probability of each treatment being ranked 1st, 2nd, etc. for each ranked parameter can also be plotted using cumrank(). These can be used to easily compare how different treatments rank for each ranked parameter simultaneously. By default, the Surface Under the Cumulative Ranking curve (SUCRA) are also returned for each treatment and ranked parameter (Salanti, Ades, and Ioannidis 2011).

# Cumulative ranking for all ranked parameters
cumrank(ranks)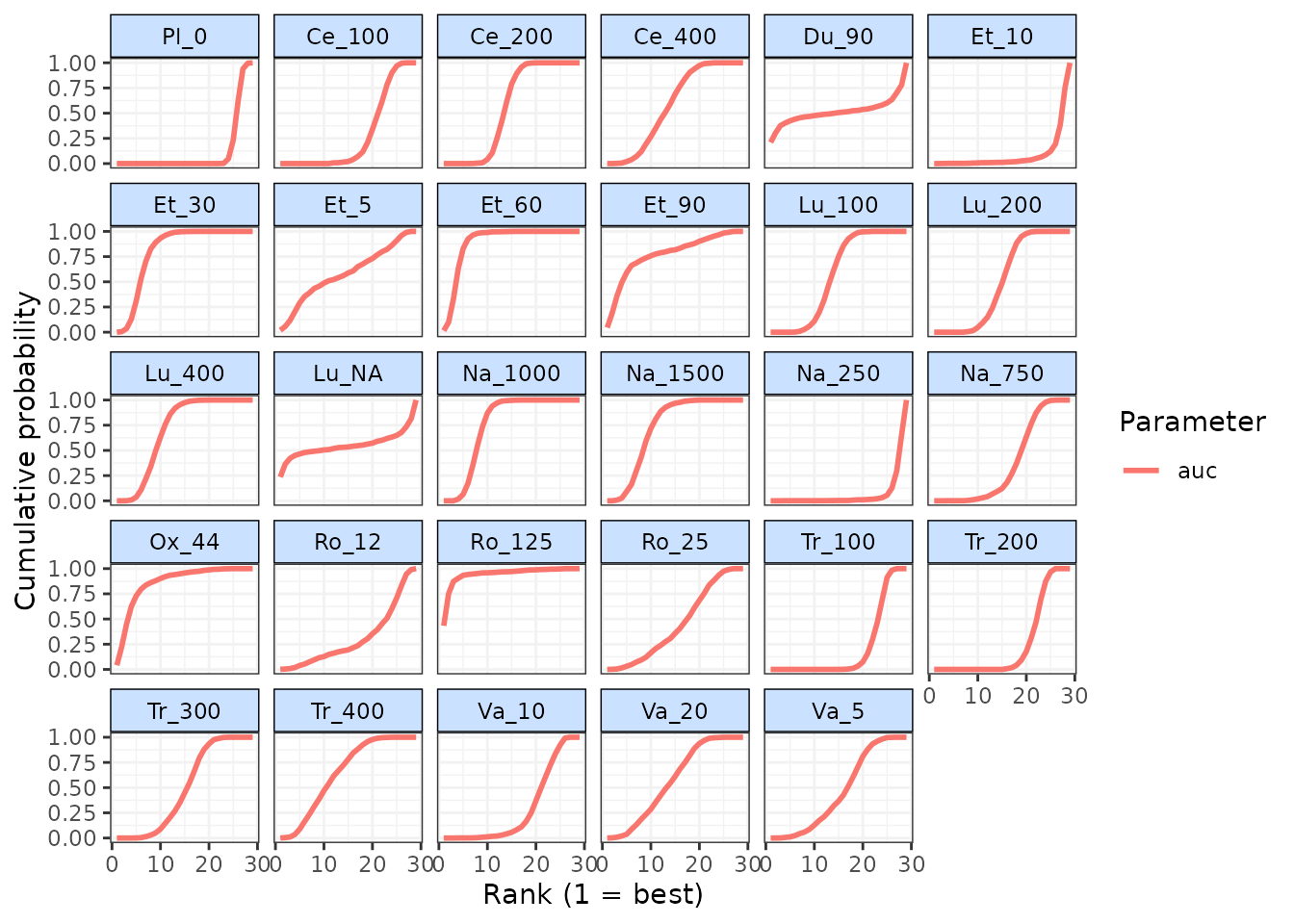

#> # A tibble: 29 × 3
#>    treatment parameter  sucra
#>    <fct>     <chr>      <dbl>
#>  1 Pl_0      auc       0.115 
#>  2 Ce_100    auc       0.278 
#>  3 Ce_200    auc       0.537 
#>  4 Ce_400    auc       0.559 
#>  5 Du_90     auc       0.499 
#>  6 Et_10     auc       0.0822
#>  7 Et_30     auc       0.786 
#>  8 Et_5      auc       0.569 
#>  9 Et_60     auc       0.870 
#> 10 Et_90     auc       0.751 
#> # ℹ 19 more rows

References

Salanti, G., A. E. Ades, and J. P. Ioannidis. 2011. “Graphical Methods and Numerical Summaries for Presenting Results from Multiple-Treatment Meta-Analysis: An Overview and Tutorial.” Journal Article. J Clin Epidemiol 64 (2): 163–71. https://doi.org/10.1016/j.jclinepi.2010.03.016.