MBNMAdose: Perform Network Meta-Regression

Network meta-regression

Study-level covariates can be included in the model to adjust treatment effects following an approach for meta-regression outlined in NICE Technical Support Document 3 (Dias et al. 2011). This can be used to explore and account for potential effect modification.

Following the definition in NICE Technical Support Document 3, network meta-regression can be expressed as an interaction on the treatment effect in arms $\geq2$ :

$\theta_{i,k}=\mu_i+(f(x,\beta_{a_{i,k}})-f(x,\beta_{a_{i,1}})) + (\psi_{1,a_{i,k}}-\psi_{1,a_{i,1}})$

where $\theta_{i,k}$ is the linear predictor, $\mu_{i}$ is the baseline effect on arm 1, $f(x,\beta_{a_{i,k}})$ is the dose-response function at dose $x$ with dose-response parameters $\beta_{a_{i,k}}$ for agent $a$ in arm $k$ of study $i$ . $\psi_{1,a_{i,k}}$ is then the effect modifying interaction between the agent in arm $k$ and the network reference agent (typically Placebo in a dose-response analysis).

Data preparation

To improve estimation:

continuous covariates should be centred around their mean
binary/categorical variables should be recoded with the most commonly reported value as the reference category

# Using the SSRI dataset
ssri.reg <- ssri

# For a continuous covariate
ssri.reg <- ssri.reg %>%
    dplyr::mutate(x.weeks = weeks - mean(weeks, na.rm = TRUE))

# For a categorical covariate
table(ssri$weeks)  # Using 8 weeks as the reference
ssri.reg <- ssri.reg %>%
    dplyr::mutate(r.weeks = factor(weeks, levels = c(8, 4, 5, 6, 9, 10)))

# Create network object
ssrinet <- mbnma.network(ssri.reg)
#> Values for `agent` with dose = 0 have been recoded to `Placebo`
#> agent is being recoded to enforce sequential numbering

Modelling

For performing network meta-regression, different assumptions can be made regarding how the effect modification may be shared across agents:

Independent, agent-specific interactions

The least constraining assumption available in MBNMAdose is to assume that the effect modifier acts on each agent independently, and separate $\psi_{1,a_{i,k}}$ are therefore estimated for each agent in the network.

A slightly stronger assumption is to assume that agents within the same class share the same interaction effect, though classes must be specified within the dataset for this.

# Regress for continuous weeks Separate effect modification for each agent vs
# Placebo
ssrimod.a <- mbnma.run(ssrinet, fun = dfpoly(degree = 2), regress = ~x.weeks, regress.effect = "agent")

summary(ssrimod.a)
#> ========================================
#> Dose-response MBNMA
#> ========================================
#> 
#> Likelihood: binomial
#> Link function: logit
#> Dose-response function: fpoly
#> 
#> Pooling method
#> 
#> Method: Common (fixed) effects estimated for relative effects
#> 
#> 
#> beta.1 dose-response parameter results
#> 
#> Pooling: relative effects for each agent
#> 
#> |Agent        |Parameter |  Median|    2.5%|   97.5%|
#> |:------------|:---------|-------:|-------:|-------:|
#> |citalopram   |beta.1[2] | -0.0905| -0.3472|  0.1787|
#> |escitalopram |beta.1[3] |  0.1313| -0.1387|  0.4076|
#> |fluoxetine   |beta.1[4] |  0.2670|  0.0301|  0.4954|
#> |paroxetine   |beta.1[5] | -0.1325| -0.4393|  0.1681|
#> |sertraline   |beta.1[6] |  1.2071| -8.0971| 10.5708|
#> 
#> 
#> beta.2 dose-response parameter results
#> 
#> Pooling: relative effects for each agent
#> 
#> |Agent        |Parameter |  Median|    2.5%|  97.5%|
#> |:------------|:---------|-------:|-------:|------:|
#> |citalopram   |beta.2[2] |  0.0664| -0.0047| 0.1384|
#> |escitalopram |beta.2[3] | -0.0062| -0.0943| 0.0782|
#> |fluoxetine   |beta.2[4] | -0.0653| -0.1316| 0.0031|
#> |paroxetine   |beta.2[5] |  0.0898| -0.0050| 0.1884|
#> |sertraline   |beta.2[6] | -0.1688| -1.1868| 0.8442|
#> 
#> 
#> power.1 dose-response parameter results
#> 
#> Assigned a numeric value: 0
#> 
#> power.2 dose-response parameter results
#> 
#> Assigned a numeric value: 0
#> 
#> Meta-regression
#> 
#> Covariates interacting with study-level relative effects: x.weeks
#> Common (identical) covariate-by-agent effects
#> 
#> 
#> |Agent        |Parameter    |  Median|     2.5%|   97.5%|
#> |:------------|:------------|-------:|--------:|-------:|
#> |citalopram   |B.x.weeks[2] | -0.1601|  -0.3384|  0.0164|
#> |escitalopram |B.x.weeks[3] |  0.1603|  -0.0356|  0.3581|
#> |fluoxetine   |B.x.weeks[4] | -0.0316|  -0.1713|  0.1084|
#> |paroxetine   |B.x.weeks[5] |  0.0862|  -0.0235|  0.1936|
#> |sertraline   |B.x.weeks[6] |  1.2913| -18.3645| 20.9489|
#> 
#> 
#> Model Fit Statistics
#> Deviance = 890.8
#> Residual deviance = 191.1
#> Deviance Information Criterion (DIC) = 966.4

Within the output, a separate parameter (named B.x.weeks[]) has been estimated for each agent that corresponds to the effect of an additional week of study follow-up on the relative effect of the agent versus Placebo. Note that due to the inclusion of weeks as a continuous covariate, we are assuming a linear effect modification due to study follow-up.

Random effect interaction

Alternatively, the effect modification for different agents versus the network reference agent can be assumed to be exchangeable/shared across the network about a common mean, $\hat{\psi}$ , with a between-agent standard deviation of $\tau_\psi$ :

$\psi_{1,a_{i,k}} \sim N(\hat{\psi}, \tau^2_\psi)$

# Regress for continuous weeks Random effect modification across all agents vs
# Placebo
ssrimod.r <- mbnma.run(ssrinet, fun = dfpoly(degree = 2), regress = ~x.weeks, regress.effect = "random")

summary(ssrimod.r)
#> ========================================
#> Dose-response MBNMA
#> ========================================
#> 
#> Likelihood: binomial
#> Link function: logit
#> Dose-response function: fpoly
#> 
#> Pooling method
#> 
#> Method: Common (fixed) effects estimated for relative effects
#> 
#> 
#> beta.1 dose-response parameter results
#> 
#> Pooling: relative effects for each agent
#> 
#> |Agent        |Parameter |  Median|    2.5%|  97.5%|
#> |:------------|:---------|-------:|-------:|------:|
#> |citalopram   |beta.1[2] | -0.0508| -0.4208| 0.2349|
#> |escitalopram |beta.1[3] |  0.2452| -0.0534| 0.5715|
#> |fluoxetine   |beta.1[4] |  0.2807|  0.0184| 0.5190|
#> |paroxetine   |beta.1[5] | -0.1117| -0.4571| 0.2104|
#> |sertraline   |beta.1[6] |  0.6415|  0.1647| 1.2119|
#> 
#> 
#> beta.2 dose-response parameter results
#> 
#> Pooling: relative effects for each agent
#> 
#> |Agent        |Parameter |  Median|    2.5%|   97.5%|
#> |:------------|:---------|-------:|-------:|-------:|
#> |citalopram   |beta.2[2] |  0.0572| -0.0212|  0.1604|
#> |escitalopram |beta.2[3] | -0.0358| -0.1457|  0.0652|
#> |fluoxetine   |beta.2[4] | -0.0681| -0.1375|  0.0123|
#> |paroxetine   |beta.2[5] |  0.0876| -0.0148|  0.1970|
#> |sertraline   |beta.2[6] | -0.1088| -0.2280| -0.0111|
#> 
#> 
#> power.1 dose-response parameter results
#> 
#> Assigned a numeric value: 0
#> 
#> power.2 dose-response parameter results
#> 
#> Assigned a numeric value: 0
#> 
#> Meta-regression
#> 
#> Covariates interacting with study-level relative effects: x.weeks
#> Random (exchangeable) covariate-by-treatment effects
#> 
#> 
#> |Regression effect |Parameter | Median|    2.5%|  97.5%|
#> |:-----------------|:---------|------:|-------:|------:|
#> |Random effect     |B.x.weeks | 0.0254| -0.0664| 0.1221|
#> 
#> 
#> Standard deviation for random covariate-by-treatment effects
#> 
#> |Parameter    | Median|   2.5%|  97.5%|
#> |:------------|------:|------:|------:|
#> |sd.B.x.weeks | 0.0637| 0.0026| 0.2297|
#> 
#> 
#> Model Fit Statistics
#> Deviance = 891.5
#> Residual deviance = 191.8
#> Deviance Information Criterion (DIC) = 980.4

In this case only a single regression paramter is estimated (B.x.weeks), which corresponds to the mean effect of an additional week of study follow-up on the relative effect of an active agent versus Placebo. A parameter is also estimated for the between-agent standard deviation, sd.B.x.weeks.

Common effect interaction

This is the strongest assumption for network meta-regression, and it implies that effect modification is common (equal) for all agents versus the network reference agent:

$\psi_{1,a_{i,k}} =\hat{\psi}$

# Regress for categorical weeks Common effect modification across all agents vs
# Placebo
ssrimod.c <- mbnma.run(ssrinet, fun = dfpoly(degree = 2), regress = ~r.weeks, regress.effect = "common")

summary(ssrimod.c)
#> ========================================
#> Dose-response MBNMA
#> ========================================
#> 
#> Likelihood: binomial
#> Link function: logit
#> Dose-response function: fpoly
#> 
#> Pooling method
#> 
#> Method: Common (fixed) effects estimated for relative effects
#> 
#> 
#> beta.1 dose-response parameter results
#> 
#> Pooling: relative effects for each agent
#> 
#> |Agent        |Parameter |  Median|    2.5%|  97.5%|
#> |:------------|:---------|-------:|-------:|------:|
#> |citalopram   |beta.1[2] | -0.0686| -0.3486| 0.1968|
#> |escitalopram |beta.1[3] |  0.2473|  0.0215| 0.4695|
#> |fluoxetine   |beta.1[4] |  0.2193| -0.0241| 0.4693|
#> |paroxetine   |beta.1[5] | -0.1097| -0.4053| 0.1955|
#> |sertraline   |beta.1[6] |  0.5893|  0.1109| 1.0744|
#> 
#> 
#> beta.2 dose-response parameter results
#> 
#> Pooling: relative effects for each agent
#> 
#> |Agent        |Parameter |  Median|    2.5%|   97.5%|
#> |:------------|:---------|-------:|-------:|-------:|
#> |citalopram   |beta.2[2] |  0.0592| -0.0127|  0.1338|
#> |escitalopram |beta.2[3] | -0.0288| -0.1054|  0.0488|
#> |fluoxetine   |beta.2[4] | -0.0561| -0.1259|  0.0128|
#> |paroxetine   |beta.2[5] |  0.0855| -0.0100|  0.1809|
#> |sertraline   |beta.2[6] | -0.1017| -0.1979| -0.0047|
#> 
#> 
#> power.1 dose-response parameter results
#> 
#> Assigned a numeric value: 0
#> 
#> power.2 dose-response parameter results
#> 
#> Assigned a numeric value: 0
#> 
#> Meta-regression
#> 
#> Covariates interacting with study-level relative effects: r.weeks4, r.weeks5, r.weeks6, r.weeks9, r.weeks10
#> Common (identical) covariate-by-treatment effects
#> 
#> 
#> |Regression effect |Parameter   |  Median|    2.5%|   97.5%|
#> |:-----------------|:-----------|-------:|-------:|-------:|
#> |Common effect     |B.r.weeks10 |  0.1504| -0.2455|  0.5443|
#> |Common effect     |B.r.weeks4  | -0.7459| -1.4320| -0.0630|
#> |Common effect     |B.r.weeks5  |  0.8323| -0.1496|  1.8133|
#> |Common effect     |B.r.weeks6  |  0.0535| -0.1387|  0.2462|
#> |Common effect     |B.r.weeks9  |  0.4415| -0.3891|  1.3221|
#> 
#> 
#> Model Fit Statistics
#> Deviance = 891.2
#> Residual deviance = 191.5
#> Deviance Information Criterion (DIC) = 964.2

In this case we have performed the network meta-regression on study follow-up (weeks) as a categorical covariate. Therefore, although only a single parameter is estimated for each effect modifying term, there is a separate term for each category of week and a linear relationship for effect modification is no longer assumed.

Alternative assumptions

Although this is beyond the capability of MBNMAdose, one could envision a more complex model in which the interaction effect also varied by a dose-response relationship, rather than assuming an effect by agent/class or across the whole network. This would in principle contain fewer parameters than a fully independent interaction model (in which a separate regression covariate is estimated for each treatment in the dataset).

Aggregation bias

Note that adjusting for aggregated patient-level covariates (e.g. mean age, % males, etc.) whilst using a non-identity link function can introduce aggregation bias. This is a form of ecological bias that biases treatment effects towards the null and is typically more severe where treatment effects are strong and where the link function is highly non-linear (Dias et al. 2011). This can be resolved by performing a patient-level regression, but Individual Participant Data are required for this and such an analysis is outside the scope of MBNMAdose.

Prediction using effect modifying covariates

Models fitted with meta-regression can also be used to make predictions for a specified set of covariate values. This includes when estimating relative effects using get.relative(). An additional argument regress.vals can be used to provide a named vector of covariate values at which to make predictions.

# For a continuous covariate, make predictions at 5 weeks follow-up
pred <- predict(ssrimod.a, regress.vals = c(x.weeks = 5))
plot(pred)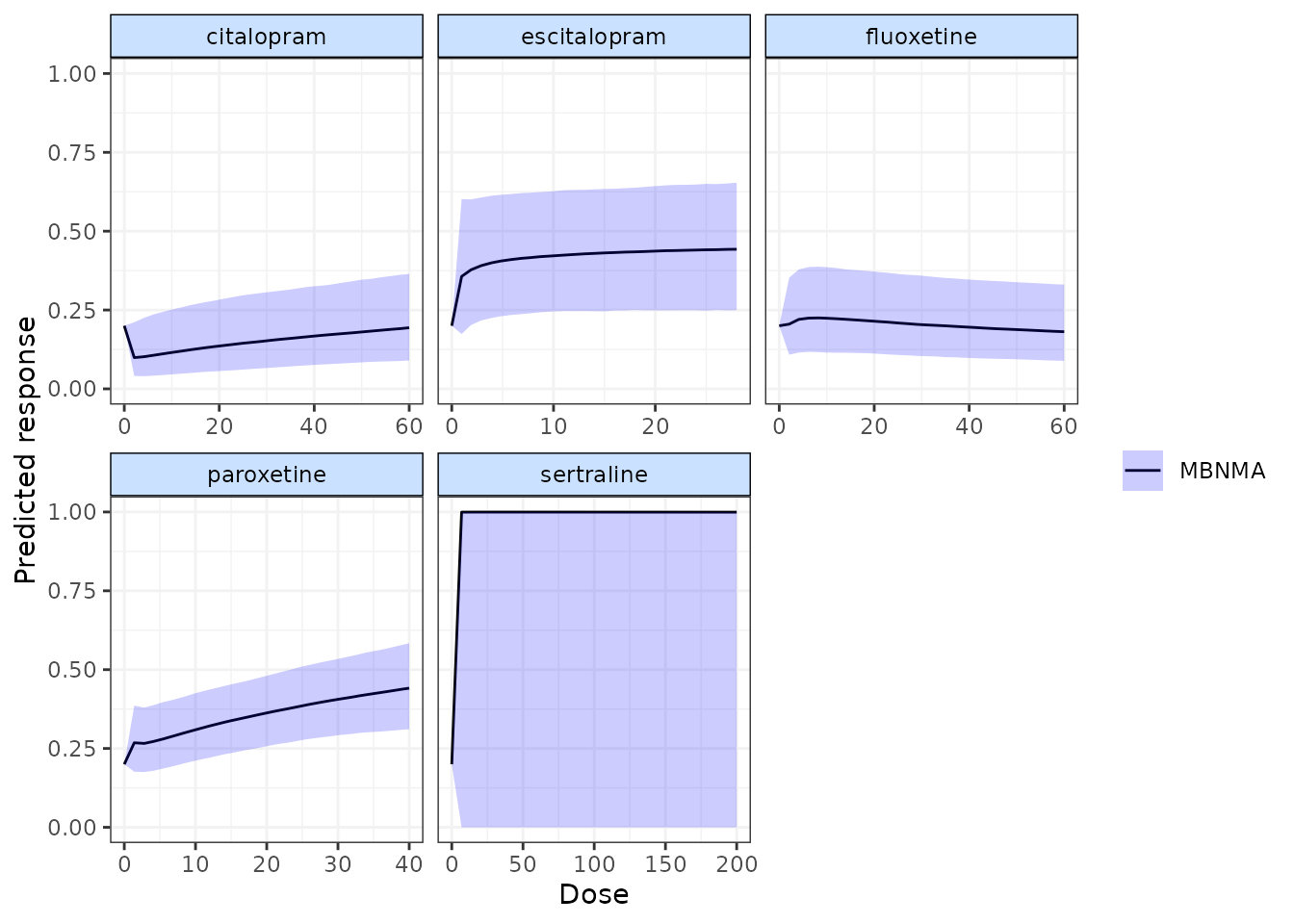

Predictions are very uncertain for Sertraline, as studies only investigated this agent at 6 weeks follow-up and therefore the agent-specific effect modification is very poorly estimated.

# For a categorical covariate, make predictions at 10 weeks follow-up
regress.p <- c(r.weeks10 = 1, r.weeks4 = 0, r.weeks5 = 0, r.weeks6 = 0, r.weeks9 = 0)

pred <- predict(ssrimod.c, regress.vals = regress.p)
plot(pred)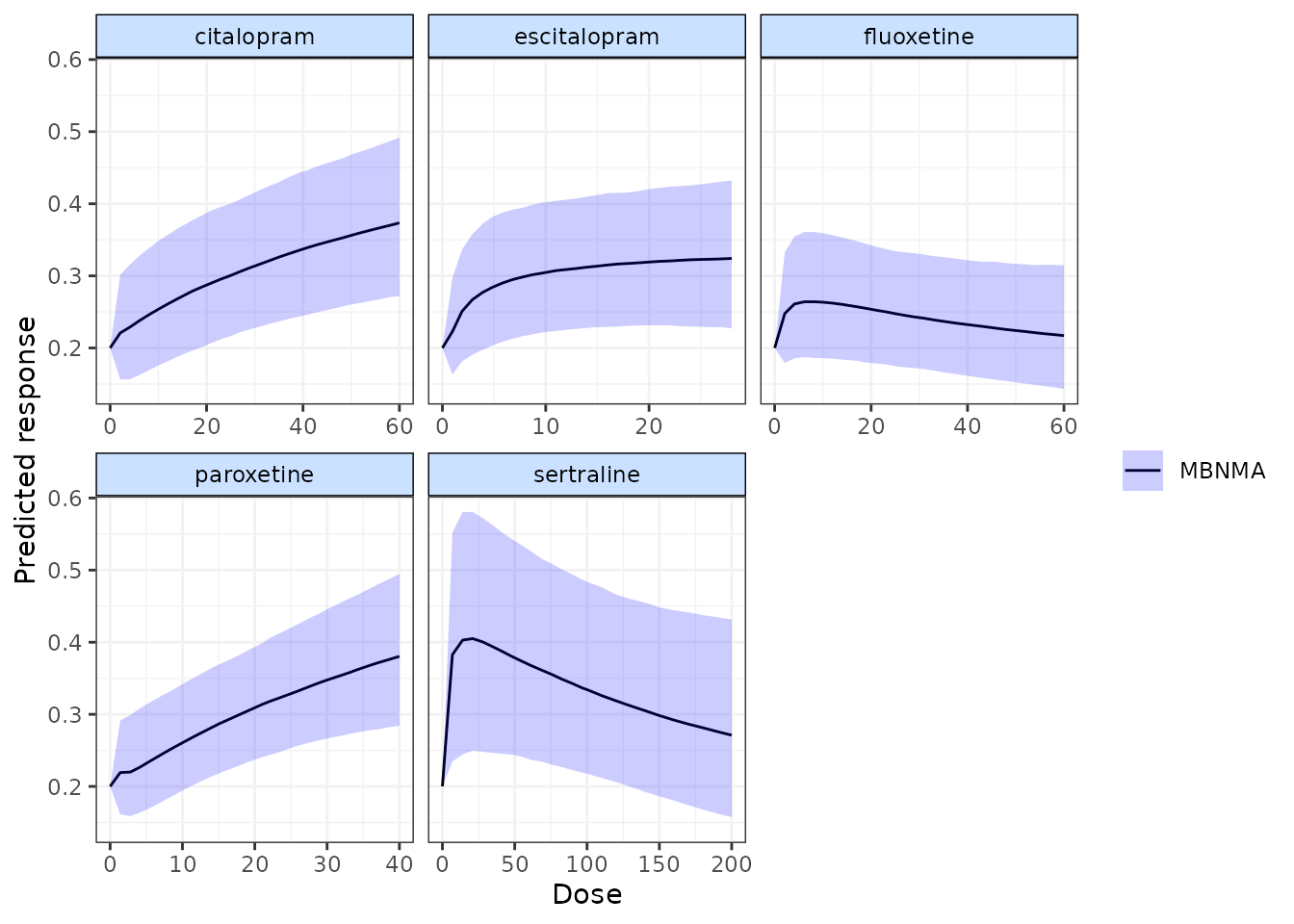

Note that categorical covariates are modelled as multiple binary dummy covariates, and so a value for each of these must be included.

References

Dias, S., A. J. Sutton, N. J. Welton, and A. E. Ades. 2011. “NICE DSU Technical Support Document 3: Heterogeneity: Subgroups, Meta-Regression, Bias and Bias, Adjustment.” Decision Support Unit, ScHARR, University of Sheffield. https://www.ncbi.nlm.nih.gov/books/NBK395886/pdf/Bookshelf_NBK395886.pdf.

Hugo Pedder

2025-02-06